rajfotografie

Gulden snede

Deze regel is ontstaan in de Griekse Oudheid en is van oorsprong een wiskundig probleem uit de Euclidische meetkunde. De Gulden Snede verdeelt een lijn in twee delen waarbij de twee delen in een bepaalde rekenkundige verhouding tot elkaar staan. Die verhouding is gebaseerd op het 'gulden getal' of het getal Phi (niet Pi!). Phi heeft de waarde 1.618033998874989 et cetera.

Hoe bepaal je de Gulden Snede?

Om de Gulden Snede te bepalen verdeel je een lijnstuk AB in twee delen waarbij de lengte van beide delen zo is dat het grootste lijnstuk AC en het kleinste lijnstuk BC gelijk is aan de verhouding tussen de hele lijn AB en het langste stuk AC.

wiskundige

Een wiskundige zou het zo opschrijven. Het punt waar het lijnstuk AB in tweeën wordt verdeeld ligt daar waar AC:BC=AB:AC. Precies op dat verdeelpunt (C) is dan lijnstuk AC 1,618.. keer zo groot als lijnstuk BC en lijnstuk AB 1,618.. keer zo groot als lijnstuk AC!

betekenis

De betekenis van de Gulden Snede als compositieregel ontstaat pas in de jaren dertig van de 19e eeuw. De regel werd toen voor het eerst onderkend en gebruikt als indelingscriterium voor de compositie in de schilderkunst en de architectuur.

Gulden Snede en Regel van Derden

Omdat de verhouding tussen de lijnstukken in de Gulden Snede niet precies gelijk is en de lijn daarom ook niet in gelijke stukken opdeelt, wijkt de indeling van de Gulden Snede iets af van die van de Regel van Derden.

De volgende afbeeldingen laten de afwijking zien. De eerste afbeelding is de Regel van Derden.

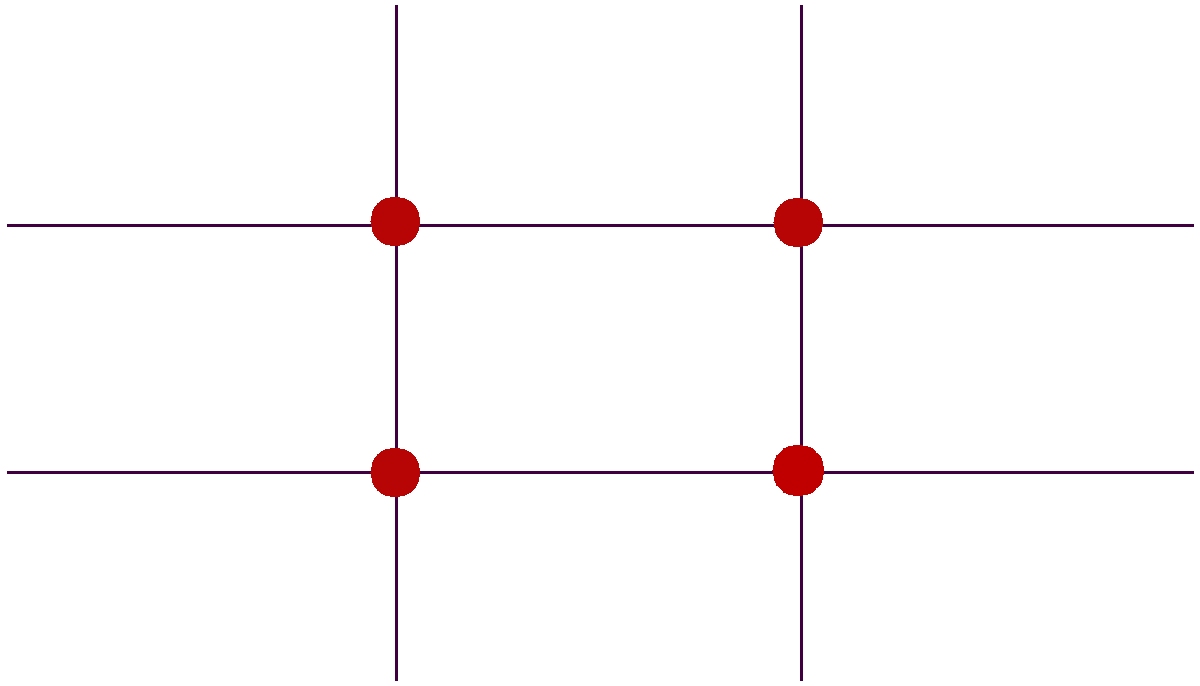
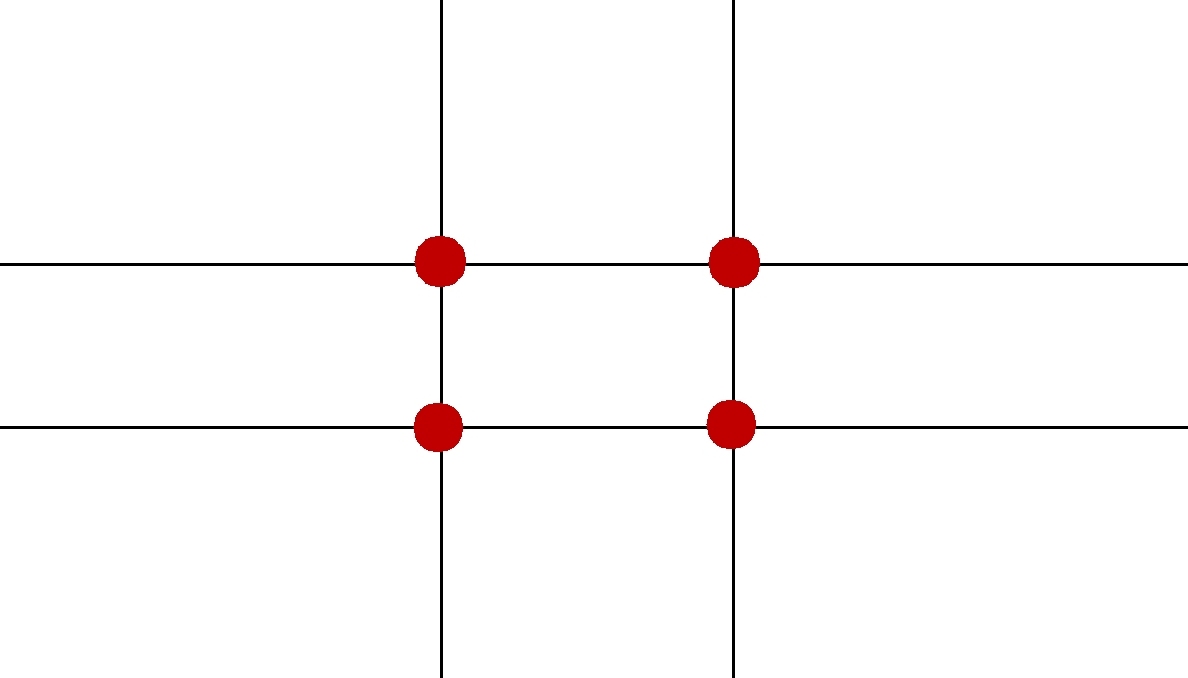
Beide regels verdelen het beeldvlak in 9 gelijke delen waarbij de Gulden Snede door de andere verhouding de snijpunten iets dichter bij elkaar zet. Voor de compositie maakt dit uiteindelijk niet echt veel uit.

aandachtspunten

Wanneer de belangrijkste aandachtspunten op de snijpunten zijn geplaatst zal de aandacht van de kijker hier naartoe geleid worden, net zoals bij de Regel van Derden.

Oorsprong Gulden Snede?

De Gulden Snede, ook wel de 'divina proportia' genoemd, komt in de natuur veel voor. Of de Gulden Snede ontdekt werd door bestudering van patronen in de natuur of dat het juist omgekeerd was, eerst de mathematische ontdekking en daarna de herkenning in natuurlijke patronen? Wie zal het zeggen. In ieder geval is het een verhouding die erg veel voorkomt en ook toepassing vindt in onder meer de architectuur.

Fibonacci

Een naam die altijd weer opduikt bij de Gulden Snede is die van Fibonacci, een Italiaanse wiskundige die leefde van 1170 tot ongeveer 1250 en waarschijnlijk in de Arabische wereld een bijzonder reeks getallen leerde kennen.

rij getallen

Leonardo Fibonacci schrijft over een rij getallen die iets bijzonders heeft. Elk getal in deze rij is gelijk aan de som van de twee voorgaande getallen. Deze reeks die in 1202 bekend werd, heette daarna de Fibonacci-reeks. De rij getallen ziet er zo uit:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 ... enz.

De rij zet zich voort door steeds de laatste twee op te tellen enzovoort. De regel dat de som van de twee voorgaande getallen een getal uit de reeks vormt gaat niet op voor de eerste twee getallen. Dat kan ook niet omdat er geen of onvoldoende voorgaande getallen zijn en nul is nul!

Het is een hele vreemde reeks waarmee verrassende berekeningen gemaakt kunnen worden. Zo is de som van iedere tien opeenvolgende getallen deelbaar door elf.

Test: de som van de eerste tien getallen is 88 en dus deelbaar door elf. De som van de getallen 11 t/m 20 (laatste waarde 4181) is 10875 wat ook weer deelbaar is door elf (987).

Er zijn meer vreemde eigenschappen zoals de herhaling van eindwaarden om de zestig waarden in de reeks.

Relatie Fibonacci en Gulden Snede

Bij de Divina Proportia of Gulden Snede is de verhouding tussen de lijnstukken steeds 1.618. Deel je de getallen van de Fibonaccireeks op elkaar dan komt is het antwoord ook steeds heel dicht bij 1.618! Het getal Phi verbindt beide begrippen dus met elkaar.

test

We doen een test: 89/55=1,618 en 21/13=1,616. 233/144=1,618 en 8/5=1.6! Er zijn heel kleine verschillen maar opvallend is de overeenkomst in uitkomsten.

Tot slot ...

De Gulden Snede en de Fibonacci-reeks hebben dus iets gemeen. In de figuur is de Gulden Snede weergegeven. De krul is een logaritmische curve die de verdeling van de lijnstukken volgt. Ieder groot blok is 1.681 maal groter dan het naastliggende kleinere blok.

De logaritmische curve of gewoonweg spiraal, zie je terug in bloemen, architectonische vlakverdelingen en in de schilderkunst. Zelfs de verhoudingen in de Mona Lisa volgen dit patroon.

samengevat

De Gulden Snede is een bijzondere en ook natuurlijke compositieregel. Fotografen gebruiken de regel om een evenwichtige verdeling van beeldelementen te krijgen. De Regel van Derden is vergelijkbaar maar mathematisch veel eenvoudiger!